What is an acid? What is a base? Measurement!

"An acid is a proton donor "
   

By this we mean that an acid can donate a proton to another substance. The `acceptor' of the proton is otherwise known as a base . (The common term is the "conjugate base").

There are many other definitions of an acid, from the pragmatic (something that makes a solution more acidic), to the obscure (Lewis' "potential electron pair acceptor"). We won't allow ourselves to get bogged down in definitions.

We will next concern ourselves with pH. Textbooks often define "pH" as

"The log 10  of the reciprocal of the hydrogen ion 
 concentration"

Not only is this definition confusing but it's technically not even correct! It's only when we come to measuring pH that we realise why this convoluted measure is commonly used. Years ago, pH meters were invented, and, as it happens, they give us values that change proportional to the log of the hydrogen ion activity. We say activity , and not concentration, for if we are pedantic, then activity and concentration are not synonyms.

By activity, we mean the measurable effect of the ion in solution. Often, there "seem to be fewer ions than there actually are". For example, we believe that if there are say five hydrogen ions in a volume of water, then the activity probably only reflects four of these --- the "activity coefficient" is four fifths, or 0.8.

In fact, when we're talking acid-base, we should always be talking about activities of the various ions. Fortunately, modern laboratories are almost always reporting activity when they provide us with, say, a serum sodium!

Another thing you may have spotted is that in our initial definition, we talked about the reciprocal of the hydrogen ion concentration. One benefit of using the reciprocal is to get rid of the negative sign that otherwise results. Remember that log(1/x) is the same as -log(x).

It's probably better to continue use our convoluted pH terminology, if only because it's time-hallowed, and a pH of 7.44 is probably more familiar to most than a "hydrogen ion concentration/activity" of 36nmol/l, or whatever.

The glass pH electrode

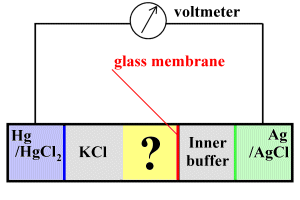
In the above sketch, the sample (yellow) occupies the compartment labelled with a question mark. On the one side, a potassium chloride bridge connects the sample electrically to a reference (calomel) electrode which uses mercury and mercuric chloride to generate a reference voltage. On the other side, a thin glass electrode separates the sample and a buffer solution, which is in turn in contact with a second electrode that utilises silver/silver chloride.

The idea is that the thin glass membrane is permeable to hydrogen ions, which can diffuse across it to the inner buffer solution. When they do so, the voltage at the Ag/AgCl electrode changes. We can compare this voltage at the silver electrode with the constant voltage at the Hg/HgCl ₂ electrode --- because voltage change varies with the pH, we can get a read-out of pH.

There are several cautions:

1. The system is temperature dependent (We know that pH of water varies with temperature, for starters), so must be kept at a constant temperature, usually 37 ^o C;
2. For a variety of reasons, the system needs calibration , and this calibration must be performed fairly frequently. Voltage differences are compared to the values obtained with two calibration solutions, one with a pH of about 6.84, a second with a higher pH of 7.38. The clinical relevance of this is that one should regard high pH readings e.g. 7.6 with a certain degree of suspicion, as they represent extrapolations above the upper calibration point!
3. Practically, the KCl bridge connecting in the calomel electrode is usually placed distally to prevent the potassium and chloride ions (some of which will diffuse into the sample) from interfering with measurement. KCl is used because potassium and chloride ions diffuse at about the same rate in aqueous solutions.
4. A voltmeter that draws significant current will completely mess up measurement! In other words, current flow must be limited by having a voltmeter with an incredibly high input impedance , typically about 100 million Ohms.
5. Note that the glass electrode is not perfect, and small amounts of other ions apart from H ⁺ will cross.

We will not here explore the details of why dipping a metal into an electrolyte solution (for example Ag and AgCl) results in a potential (electromotive force) being generated at the interface, but the principle is that seen in any battery!

The bottom line is that for every change in pH of one pH unit, the measured voltage changes by about 60 mV. In defining a pH standard (to which we can trace back our calibration of an instrument) a somewhat different system is used, the hydrogen electrode, but the difference in voltage (emf) is very similar, at 59.16mV (but this is at 25 ^o C, not the 37 degrees of our system).

Why do we care about pH?

pH is vitally important in body processes for many reasons, mainly because most metabolic processes are directly or indirectly affected by changes in pH. This is because pH alterations affect not only reactions involving small molecules in which hydrogen ions participate on one side of the reaction, but also affect complex things like protein folding and charge on the side groups of amino acids within proteins.

Why so many cellular metabolic compounds are acids or bases is explained by the Davis hypothesis, which says that their acidic/basic properties result in these compounds being ionised at cellular pH, and this means that they don't move readily across membranes. The cell can keep these compounds where it wants them owing to the lipophilic cell membrane, which traps such ions inside the cell!

Alpha-stat

An interesting extension of the Davis hypothesis is that intracellular pH is normally maintained around the point where the concentration of hydrogen and hydroxyl ions is equal. At 37 ^o , this pH is about 6.8 --- note that, although we commonly think of a neutral pH as being 7.0, this is only in water at 25 ^o C! There is really only one constituent of proteins that is responsible for the remarkably constant intracellular balance between [H ⁺] and [OH ^-] as the temperature varies. This is histidine, with its imidazole side-chain. The degree of dissociation of the imidazole group of histidine is about 0.55, and this value (often called "alpha") doesn't change appreciably with temperature. The reason why alpha doesn't change is because the pKa of the imidazole does vary with temperature. The theory that alpha remains constant with temperature variations is termed the "imidazole alpha-stat hypothesis".

It appears that the body rigorously maintains alpha-stat. This maintenance includes keeping the CO ₂ content of the blood constant with varying temperature. (A perturbation of CO ₂ content would alter alpha).

Some clinicians pooh-pooh alpha-stat, and try to force the body to maintain a constant pH whatever the body temperature, in circumstances such as hypothermia in cardiac anaesthesia. These are the folks who temperature-correct their arterial blood gas results, a dying practice. At the end of the day, the clinical relevance arguing about pH-stat versus alpha-stat seems minute, although you can find literature vehemently supporting both approaches! A good clinical rule might be "don't fiddle".

What alters pH?

The traditional approach to acid-base balance centres around the equations that relate pH, bicarbonate concentration, and PCO ₂ . Things then become very simple, because we have really only two major options --- there may be perturbations of either:

1. PCO ₂ , resulting in respiratory acidosis or alkalosis; or
2. [HCO ₃ ^-], reflecting (some even say resulting in ) metabolic acidosis or alkalosis.

This traditional approach has the merit of relative simplicity.

We say relative simplicity, because proponents of this approach have introduced confusion at many points. The two main schools are:

1. The Boston school, who use several simple equations to quantify the relative "metabolic" and "respiratory" contributions, depending on whether the derangement in acid-base balance is "acute" or "chronic";
2. The Copenhagen school, who have introduced the concepts of "base excess" or "base deficit", and "standard bicarbonate". These measures are said to represent standardised values, which purportedly exclude any respiratory component, and give us a "pure measure" of metabolic acidosis/alkalosis.

Nuts and bolts

Whatever we feel about the above, it is clear that body pH balance is tightly controlled, and the major participants are the lungs and the kidneys. Respiratory control is used to acutely alter PCO ₂ and thus keep pH near the normal range; over the longer term, the kidney alters the balance of ions it excretes to compensate for pH derangement.

Sometimes, the control mechanisms themselves go haywire. Good examples would be where a patient primarily hyperventilates, resulting in alkalosis, or where renal dysfunction results in acidosis.

It's not unreasonable to describe a primary derangement of ventilation as a respiratory alkalosis or acidosis, and a "metabolic" derangement of pH as a metabolic acidosis , or alkalosis. We will explore common examples of such derangement below, but first let's look in more detail at the control mechanisms...

How is body pH controlled?

Traditional acid-base teaching lays great importance on the concept of buffering . The idea here is that various substances within the body, such as bicarbonate, counteract alterations in pH by their "buffering effects". This concept is built into the equations of the Stewart approach, but we've devoted a section below to the concept of buffering. Here, we will explore the major organ systems that influence pH:

The lungs

The role of the lungs is almost self-explanatory --- about 20 moles of CO ₂ are formed in the body every day, and clearly this CO ₂ must be eliminated for life to continue. The topic of respiratory control, and the response characteristics of these control mechanisms in health and disease is beyond this text. For a fair exploration of respiratory regulation of PCO ₂ , see Brandis.

Suffice it to say that impaired ventilation will result in acidosis, and excessive ventilation will result in alkalosis, but much more important is the fact that in the presence of metabolic pH derangement, these same control mechanisms will compensate for increases or decreases in pH by corresponding hypo- or hyperventilation, if at all possible.

The kidney

In the kidney the traditional approach characterises renal handling of acid-base balance as "removal of metabolically produced hydrogen ions". The body needs to get rid of superfluous sulphate and phosphate, and will do so together with a heady mix of ammonium ions, hydrogen ions, sodium and potassium. Failure to do so will result in metabolic acidosis; other derangements will result in alkalosis. The quantity of hydrogen ions normally removed is about 70--100 mmol/day.

Traditional approaches usually emphasize the "amount of bicarbonate" absorbed from glomerular ultrafiltrate by the proximal tubule of the kidney (about 4 mol/day).

Other influences: stomach, bowel, liver

Although ion and pH balance are closely regulated within the gastrointestinal tract, from time to time, GIT disorders result in disturbances of acid-base balance. Prolonged vomiting will result in loss of hydrochloric acid, and this must clearly cause alkalosis.

The influence of diarrhoea is more variable, depending on duration and what exactly is being lost, but if sodium and potassium ions, together with bicarbonate, are the predominant species being lost, it's easy to believe that this might cause acidosis.

Mention should be made briefly of the normal "alkaline tide" that flows in the bloodstream from the stomach as it actively produces acid, and the corresponding acid tide coming from the pancreas as it pours out bicarbonate, Na ⁺ and K ⁺ ions into the gut to counterbalance the stomach acid.

We should also not neglect the role of the liver. This metabolically active organ is particularly important in picking up organic anions such as lactate, which otherwise contribute to acidosis.

Focus: the H-H equation

The core of traditional acid-base teaching is the Henderson-Hasselbalch equation (Note the two l's in the frequently misspelt Hasselba l ch ). Here it is:

        pH = pK’a + log 10  ( [HCO 3 -] / (0.03 * PCO 2 ) )
   

The pK'a constant varies with temperature, but is generally taken as about 6.1. There are three steps in understanding the HH equation.

1. The law of mass action

Consider a chemical reaction where two molecular species, A and B, combine to form a third species, C. At equilibrium, we have the equilibrium reaction:

   A + B <==> C
   

The amount of C being formed will depend on the amounts of A and B present. Add more A or more of B, and the amount of C produced will increase proportionally. We might state this as:

   Rate of C formation = k1 * [A] * [B]
   

Likewise, the formation of A and B in the reverse reaction will depend only on [C], thus:

   Rate of A and B formation = k2 * [C]
   

   k2 * [C] = k1 * [A] * [B}
   

    [C] = K * [A] * [B]
   

 
    K = [C] / ( [A] * [B] )
   

Where we're looking at a system involving a weak acid, the K is usually referred to as K _a , in deference to the fact that we're dealing with an acid. Another convenience is to call the logarithm of the reciprocal of this constant pKa .

2. Let's look at CO ₂ and bicarbonate

In the case of bicarbonate, things are a little more complex, because our equations are:

   H 2 O + CO 2  <==>  H 2 CO 3 
   

 
   H 2 CO 3  <==> H + + HCO 3 -
   

   HCO 3 - <==> H + + CO 3 2-
   

The H-H simplifies things, by ignoring the CO ₃ ^2-, and the intermediate H ₂ CO ₃ , to get:

   H 2 O + CO 2  <==> H + + HCO 3 -
   

    K'a = ([H +] * [HCO 3 -] ) / [CO 2 ]
    

What we've done in the above equation is create a "lumped together" constant K'a which takes into account the intermediate step involving H ₂ CO ₃ , and the concentration of H ₂ O (which is pretty darn constant). We can rearrange the above equation to:

    1/[H +] = 1/K'a * [HCO 3 -] / [CO 2 ]
    

3. Finally, HH

All we do now is take the logarithm of both sides:

 log (1/[H +]) = log(1/K'a) + log ([HCO 3 -] / [CO 2 ])
    

Note that another way of saying log(1/K'a) is pK'a, and that we can get from PCO ₂ to [CO ₂ ] by multiplying by 0.03 mmol.l ^-1 .mmHg ^-1 , the solubility coefficient of CO ₂ in water. We now have the notorious HH equation in its usual incarnation:

        pH = pK’a + log 10  ( [HCO 3 -] / (0.03 * PCO 2 ) )
   

Why?

What is the practical value of the HH equation? The major use of the HH equation is in calculating the [HCO ₃ ^-] in a blood sample.

What is a `buffer'?

The simple idea behind "buffering" is that, if one, say, adds acid to a solution, then the buffer "mops up" some of the added hydrogen ions. Conversely, if we were to remove hydrogen ions, the buffer would also keep things steady by releasing some hydrogen ions, counteracting the perturbation. As a consequence, there is a lesser change in pH than if the buffer had not been present . For example, adding hydrogen ions to a bicarbonate/CO ₂ system in equilibrium will tend to shift the equilibrium, mopping up some hydrogen ions.

A buffer system is usually a "weak acid combined with the salt of that acid". Buffering is generally said to be maximal at or around the pKa of the weak acid, at ± 1 pH unit around the pKa. A lot of work has gone into defining things like "buffer power", which tells us how much acid (or base) must be added to a solution to change the pH by a fixed amount, such as one pH unit. Much of this effort is wasted on clinical medicine!

The major extracellular buffer is said to be the bicarbonate system. The complexity of acid-base physiology is illustrated by the fact that bicarbonate is an effective "buffer" despite physiological pH being far removed from the pKa of the bicarbonate system (6.1). Conventional acid-base theory has some trouble explaining this "buffering". Note that other factors, such as the ability to retain or blow off carbon dioxide by changing control of respiration, are used by the body to further adjust pH, but one mustn't confuse control with buffering.

It has been traditionally taught that plasma proteins (notably albumin) also provide a "buffering effect". (In fact, when one examines more accurate models like that of Stewart, we find that this is incorrect).

The relevant pKa of the intracellular phosphate system is about 6.7, explaining its utility as a buffer there. Imidazole groups on proteins also have a convenient pKa of about 6.8; this is relevant not only within the red blood cell (where haemoglobin is rich in histidine, and present in high concentrations, about a third of the red cell), but also in cells throughout the body.

When one moves into cells, things become rather complicated. Within the red cell, haemoglobin has a substantial buffering effect. But there is worse to come...

The Haldane effect

In 1914, Christiansen, Douglas and Haldane found that deoxygenated blood is far better than oxygenated blood at carrying carbon dioxide [J Physiol 1914 48 244]. They thought that the reason for this 'Haldane' effect was that deoxygenated haemoglobin is a better buffer. They were largely wrong ! It is in fact correct that deoxyhaemoglobin is a better buffer, but this is not the major reason why carriage of CO ₂ increases!

The major reason is that deoxyhaemoglobin binds more CO ₂ as carbamino compounds! This carbaminohaemoglobin in fact accounts for about one third of the difference in arterial and venous CO ₂ content! You can't really blame poor Christiansen et al too much, for carbaminohaemoglobin was only described in 1934. (For details, see Nunn, page 223).

As an aside, it seems to be a perennial source of irritation to examiners that candidates in physiology exams confuse carbaminohaemoglobin, and the totally unrelated carboxyhaemoglobin, which is formed when carbon monoxide binds avidly to haemoglobin!

Anion gap (AG)

If you look at the commonly measured ions in plasma, Na ⁺, K ⁺, Cl ^-, and HCO ₃ ^-, you'll soon spot the fact that sum of the concentrations of the positive ions outnumbers that of the negatively charged ions. To maintain charge balance, there must be hidden negative ions --- the anion gap . What are these ions?

It turns out that, although there are tiny amounts of many negative ions in normal plasma, such as phosphate and sulphate, the most important contributor to the AG is albumin! Different authorities quote different values, but a normal AG is about 8--12 mmol/l. The calculated value depends to a large extent on how good your laboratory is at accurately measuring serum chloride concentrations --- older assays were poor. You can work out that for every 10g/L of albumin rise or drop, you can correspondingly adjust the AG by about 3 mmol/l (or a smidgeon less).

A variety of hidden anions can substantially increase the AG. Perhaps the most important are ketones and lactate, but other organic anions may contribute, if your patient has, for example been drinking methanol or antifreeze. Salicylate poisoning may also increase the gap.

Practically, you should regard an AG of 16 or more with suspicion, and be frankly worried if it's over 20. A catch is if the patient is hypoalbuminaemic, where the AG may be falsely low even in the presence of lots of organic anions!

With or without K ⁺?

Many authorities leave out the potassium when they calculate AG. They normally still quote a reference range for the AG of about 8--16 mmol/l, and allow somewhat higher values if K+ is included.

Urinary AG

Brandis neatly discusses the (minor) utility of urinary AG in distinguishing between normal anion gap acidosis due to gastrointestinal bicarbonate loss, and that due to renal problems with urinary acidification. The basic idea is that if the kidney can compensate by increasing ammonium loss, urinary anion gap will diminish (owing to the larger amounts of chloride lost in the urine; we don't measure the ammonium) --- in fact, the calculated value is often negative ! If the kidney is knackered, then the urinary anion gap will be large and positive.

Base excess and standard bicarbonate

Standard bicarbonate is simply the bicarbonate value that is present when a blood sample is adjusted to a PCO ₂ of 40mmHg --- any respiratory component is `removed'. Again, Brandis has explored the concept fairly well, together with that of base excess. We have also looked at the complexities of base excess elsewhere! Once you've decided which equation you will use to actually calculate base excess, you can then have a lot of fun by plotting base excess against PCO ₂ , and further dividing this map into zones that represent the various metabolic or respiratory acid-base abnormalities. We will not do this, but leave it to the experts. Personally, we find this approach somewhat arbitrary, and perhaps slightly confusing.

Count to 4: metabolic/respiratory, acid/alkal-osis

If arterial pH is deranged, then one should describe the abnormality as either acidaemia or alkalaemia. The more general terms acidosis and alkalosis are used to describe these states, as well as the case where compensation has occurred, so pH may not be outside the normal range of pH 7.36--7.44. If compensation has occurred, one should say so, for example:

    metabolic acidosis with respiratory compensation
    

1. Metabolic acidosis

This is acidosis due to a primary metabolic abnormality. It's convenient to classify metabolic acidosis as either:

1. normal anion gap acidosis
2. high anion gap acidosis

We've already described the anion gap, and we know that there's a fairly long list of anions that may widen it. These include lactate, ketones (beta hydroxybutyrate and acetoacetate), and salicylate, but high values are also seen in methanol (—> formic acid) and ethylene glycol (—> oxalic acid) intoxication, and to a certain extent in renal failure.

Normal anion gap acidosis is a different animal, commonly seen with renal disease or gastrointestinal loss of sodium ions, potassium and bicarbonate. Similar disturbances can be seen with exogenous administration of acids or ammonium chloride, and ileal conduits.

2. Metabolic alkalosis

This disorder is commonly iatrogenic, related to administration of base (e.g. bicarbonate, milk-alkali syndrome), diuretics (most notably frusemide), hypokalaemia or hypovolaemia. Loss of acid from the stomach by ongoing vomiting (as in pyloric stenosis, hyperemesis gravidarum, or whatever) or nasogastric suction, will also contribute. Consider other less common causes such as Cushing's or hyperaldosteronism, licorice intake, the odd villous adenoma of the rectum, and even Bartter's syndrome.

Note (and note well) that the kidney is usually rather good at compensating for metabolic alkalosis, so ongoing metabolic alkalosis more or less implies that the renal compensatory mechanisms have been interfered with, often by doctors!

3. Respiratory acidosis

By far the commonest cause of a high PCO ₂ is failure of ventilation, either due to iatrogenic intervention, or failure of the respiratory muscular mechanism and its controls. Rarely, hypercarbia is due to increased production of CO ₂ (as in the malignant hypermetabolic syndrome, MH), or `exogenous' CO ₂ (rebreathing, CO ₂ insufflation into the peritoneum).

In acute respiratory acidosis, the drop in pH is somewhat attenuated by intracellular buffering mechanisms (extracellular mechanisms contribute little). In the longer term, the kidneys compensate as best they can --- you can see this compensation as "retention of bicarbonate". It should be obvious that once this metabolic renal compensation has occurred, sudden reversion to a "normal" PCO ₂ will result in an apparent metabolic alkalosis.

4. Respiratory alkalosis

There is a long list of causes of this disorder. Always look at respiratory alkalosis in the context of the PaO2 (Is the hyperventilation actually to compensate for arterial hypoxia?) and the possibility of associated lung disease. If these are not present, think of central causes related to pain, anxiety, or brain dysfunction. Finally, consider disorders such as salicylate poisoning, and don't forget iatrogenic hyperventilation in the patient on a ventilator. Oh, and of course, there's pregnancy!

Formulae

The Boston school relies on several fairly useful empirical formulae for calculating expected compensation for the various acid-base disorders. Here they are:

1. For metabolic acidosis, the "1.5+8" rule:

     Expected PCO 2  = 1.5*[HCO 3 -] + 8
     

   Units are mmHg (PCO ₂ ) and mmol/l (bicarbonate). The range of the above calculated value is often stated as ± 2 mmHg.

2. For metabolic alkalosis the "0.7+20" rule:

     Expected PCO 2  = 0.7*[HCO 3 -] + 20
     

   Units are as you would expect, and the range is ± 5 mmHg, so there is a lot of leeway !

3. In respiratory alkalosis, the empiric distinction is made between acute and chronic respiratory alkalosis. In acute respiratory alkalosis, compensation is:

     A drop in HCO 3 - of 2mmol/l for every 10mmHg decrease in PCO 2 
     

   Whereas for chronic respiratory alkalosis (2--3 days), the rule becomes:

     A drop in HCO 3 - of 5mmol/l for every 10mmHg decrease in PCO 2 
     

   Note that the bicarbonate won't drop below about 12 mmol/l.

4. Respiratory acidosis. Here a convenient "1 for 10" rule may be used, but only for acute respiratory acidosis:

     For every 10mmHg increase in PCO 2 , HCO 3 - will increase by 1 mmol/l
     

   Note how small this is in comparison with acute respiratory alkalosis . For chronic respiratory acidosis, use:

     For every 10mmHg increase in PCO 2 , HCO 3 - will increase by 4 mmol/l
     

   ... just a smidgeon less than the compensatory movement in the other direction seen with chronic respiratory alkalosis .

Why some of the above is defective!

We have elsewhere explored the Stewart approach. The attractive thing about this approach is that it provides a mathematically rigorous model of how acid-base balance works. It describes in detail how things work in plasma based on all the relevant equations, and doesn't just focus on one sixth of the problem - the Henderson-Hasselbalch equation!

Note that our comments do not imply the traditional approach is without use. In most circumstances, traditional approaches work fairly or even extremely well. The six empiric equations of the Boston school have been experimentally validated [e.g. Ann Intern Med 1967 66 312]; the Copenhagen concepts of standard bicarbonate and base excess, although somewhat flawed in certain circumstances, are still useful approximations.

A further issue is that the Stewart approach (as refined by e.g. Fencl) gives us a good conceptual model of what is happening in plasma, but at present we have no similar model of the red cell or other intracellular environments. We even suspect that at extremes of pH, the albumin molecule may alter its configuration to the point where current measurements of the Ka's of the various side groups become inappropriate. In addition, some laboratories may not be up to the quality control required to make reliable determination of all of the species involved in the Stewart calculations.

The virtue of the Boston equations is, strangely enough, their empiric nature --- they are based on observations of how real people actually behave. The flipside is that this empiricism hardly gives us confidence when we need to apply such equations in really unusual circumstances where they haven't been "validated". We anticipate that as our understanding of the Stewart model improves and modelling is extended to the intracellular environment, and combined with models of respiratory control, there may be theoretical validation or invalidation of the Boston equations.

A summary in 12 short points

1. An acid is a proton donor --- it's conjugate base accepts the proffered proton!
2. pH is a convenient logarithmic way of representing large changes in hydrogen ion activity.
3. Exam candidates should probably learn how the glass pH electrode works.
4. The body tightly regulates pH, to maintain normal metabolic functions and trap certain ions inside cells, at least, this is what we believe!
5. In examinations, an FAQ (by examiners) is buffering, especially buffering by haemoglobin (and the role of this protein in CO ₂ transport). Know this.
6. The terms acidosis and alkalosis are general terms that refer to states where the pH has changed, and either been compensated for, or not! If the blood pH is outside the normal limits of 7.36--7.44, then only are we justified in using the terms acidaemia or alkalaemia.
7. The lungs, kidney and liver are crucial to maintenance of acid-base homeostasis. For example, metabolic alkalosis doesn't usually persist unless the kidneys are somewhat whacked!
8. Derangement in lung function/control results in respiratory acidosis/alkalosis; metabolic derangement due to renal dysfunction, gastrointestinal abnormalities, or ingestion, production or failure of removal of acids (or alkali) results in metabolic acidosis/alkalosis. The body usually compensates as best it can.
9. Conventional lore lays great emphasis on the Henderson-Hasselbalch equation, and exam candidates ignore it and its derivation at their peril.
10. The anion gap is the amount of unmeasured negative ions that make up the difference (balances charge) between the measured concentrations of positive and negative ions in plasma. Normally the AG is mainly due to albumin, and about 8--12 mmol/l. The AG is important in the evaluation of metabolic acidosis , but beware of missing a high anion-gap acidosis masked by hypoalbuminaemia!
11. Compensation for acid-base derangement can be simply guesstimated using the Boston formulae:

    The Boston formulae*
    State	Rule	Formula	Range
    metabolic acidosis	1.5+8	PCO 2 (mmHg) = 1.5*bicarbonate + 8	± 2
    metabolic alkalosis	0.7+20	PCO 2 (mmHg) = 0.7*bicarbonate + 20	± 5
    acute respiratory alkalosis	2 for 10	bicarbonate (mmol/l) drops 2 mmol/l     for every 10 mmHg PCO 2 drop	?
    chronic respiratory alkalosis	5 for 10	likewise, but 5 mmol/l	?
    acute respiratory acidosis	1 for 10	bicarbonate (mmol/l) increases 1 mmol/l     for every 10 mmHg	?
    chronic respiratory acidosis	4 for 10	likewise, but 4 mmol/l	?
    * The values are derived from Brandis

12. The Stewart approach seems a little more complex, but may well be better than the conventional approach, especially for cutting through confusion. With Stewart, a low SID , high albumin concentration and/or high PCO ₂ may all contribute to acidosis; the reverse for alkalosis.

Bibliography

Apart from individual references scattered throughout the text, the following might be useful:

1. Our Stewart page!

2. Nunn J.F. Applied Respiratory Physiology , 4th ed. Butterworth-Heinemann. 1993. ISBN 0 7506 1336 X.

3. Our Respiratory physiology page.

4. Kerry Brandis' acid-base page, recently updated to reflect the Stewart approach.

5. A challenging paper by Fencl et al. [Am J Respir Crit Care Med Vol 162. pp 2246–2251, 2000]

6. John Kellum's review [Crit Care 2000, 4:6–14].