Receptors - A brief note
 Back Up
Back Up
Receptors are proteins interacting with extracellular physiological signals and converting them into intracellular effects
This definition is by no means perfect, but seems far more useful than the blurry definition you find in so many pharmacology textbooks, along the lines of 'a receptor is any functional macromolecular component of an organism to which a drug binds'. We should perhaps avoid semi-religious bickering about the 'essential nature' of receptors, and look at how well the definition works for us!
The most important concept is that the receptor:
If we accept Hucho's definition, we can identify at least four groups of receptors:
| Types of receptor | |||||
| Receptor enzymes | Ligand-gated ion channels | G-protein-coupled receptors | Transcription factors | ||
| Tyrosine phosphorylases | Other (Thr, Ser, guanyl cyclase) | ||||
| Number of transmembrane domains | 1 | 4 | 7 | -n/a- | |
| Examples | insulin, EGF, PDGF, some lymphokines | TGF beta(Ser Thr), atrial natriuretic peptide | nicotinic cholinergic receptor, GABAA, Gln, Asp & Gly receptors | Many receptors: most peptide hormones, eicosanoids, biogenic amines e.g. catecholamines | Receptors for steroid hormones, thyroid hormone, vitamin D, retinoids. |
Once we start looking at receptors in detail, and especially how they respond when we expose them to different ligands that bind to them, strange things start to happen! Exposing receptors to different molecules, singly or in combination, can give rise to a vast array of effector responses.
There are several theories about how, for example, agonists "bind to and activate" a receptor. Such theories have to explain the various effects of not only agonists, but also antagonists, partial agonists, and even inverse agonists. One such theory that seems to fit the facts rather well is as follows:
The above model is well-described in Goodman and Gilman.
Note that if we accept a more fuzzy and broad definition of a receptor, then these criteria are difficult to apply!
Such changes are not necessarily just alterations in numbers of receptors - types and activities of receptors may also change. Over- or under-stimulation of one receptor can also have profound effects on other receptors (so called "heterologous desensitization").
The term commonly used is efficacy - in other words, if two drugs occupy the same number of receptors on a tissue, and one drug elicits a greater biological response than the other drug (by its action on the receptor) then that drug has greater efficacy. {The term intrinsic activity is sometimes used to express more or less the same concept}.
A ==> B
the more A we have, the faster we form B. If we express this
mathematically, we say:
-d[A]/dt = k[A] [Equation 1]
In other words, the rate of consumption of A is proportional to
the concentration of A.
Similarly, where we have two substances A and B combining to form a
complex AB:
A + B ==> AB
the corresponding differential equation is:
-d[A]/dt = k[A][B] [Equation 2]
In other words, the rate of consumption of A depends on both the
concentration of A and the concentration of B.
Now let's consider the case where we have a ligand binding to a
receptor to form a ligand-receptor complex. Assume we have equilibrium,
so the rate of formation of LR is the same as the rate of dissociation
of LR into L + R:
We apply the law of mass action to the forward reaction, and
from Equation 2 we find:
-d[L]/dt = k1[L][R]
but we also know that because we have equilibrium,
this rate of consumption of L is equal to the rate of dissociation
of LR into its components, given by Equation 1:
-d[LR]/dt = k2[LR]
so therefore, equating the two:
We can rearrange this to:
We have a special name for the ratio k2/k1 - we call it KD,
the dissociation constant. To get a feel for what KD means,
consider the case where exactly half of the receptors are occupied by
ligand. Then the other half of the receptors are not occupied,
so [R] = [LR], and therefore [L] = KD. Another way of saying
this is that "KD is the concentration of ligand that
at equilibrium will cause half the receptors to be ligand-bound". It's
clear from this that the more tiny the KD, the more receptors are
occupied at a given concentration of ligand - that is, the higher the
affinity of the receptors for the ligand.
Which is another way of saying: We know from its definition that KD is given by:
So if we rearrange to get an equation describing [LR]
and then substitute this in Equation 3, we get:
Why are pharmacologists so interested in the fractional occupancy?
Well, it makes sense that the effect of a drug should depend on
the fraction of receptors that are actually occupied. So the
measured effect should depend on the fractional occupancy, which
in turn should depend on [L] / ( KD + [L] ). Also, if
we have measured the maximum effect (where almost 100% of the receptors are
occupied) and we know the fractional occupancy, then we can determine
the effect for any given concentration of a ligand. This effect will
be given by:
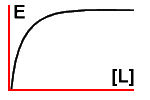
If you sit down and plot a graph of effect versus [L] you'll soon
see that we get a simple rectangular hyperbola:
The advantage is that we can now compare different ligands, and
even examine the case where we add (for example) a partial agonist
to a preparation containing a full agonist.
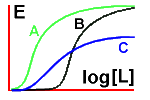
Let's first compare three drugs, A, B and C:
You can see that drug A is more potent than the other two, and
that the maximal response for drug C is less than that for the other
two - drug C is a partial agonist when compared with drug A or drug B.
Next, let's look at the effect on drug A of adding a
competitive antagonist (X) and then a non-competitive antagonist (Y).
See how increasing concentrations of drug A can overcome the effect of
the competitive antagonist, but not that of the non-competitive one!
k1 (forward) Ligand + Receptor <=======> Ligand-receptor complex k2 (backwards) Fractional occupancy
Pharmacologists often use the term fractional occupancy to
describe the fraction of receptors occupied at a particular ligand
concentration. It's obvious that the fractional occupancy is:
Use graphs to compare drugs
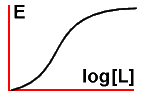
Pharmacologists are never happy with simplicity. No, that's unfair.
There's a darn good reason why they often alter the above graph, plotting
the log of the ligand concentration on the x axis, and this is
because they often need to draw graphs that involve concentrations of
ligand that vary by several orders of magnitude. If we draw the graph
thus we get a sigmoid curve:
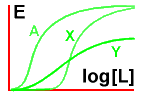
Conclusion
We've attempted to cover receptor basics, but there's lots more. Consult
the following references for further information - for example,
it's interesting to
work out the KD of an antagonist using the Schild regression,
and to understand how Saturation Radioligand Assays work!
References
Last update: 17 November 1999
Web page author
jo@anaesthetist.com